Squaring the Circle

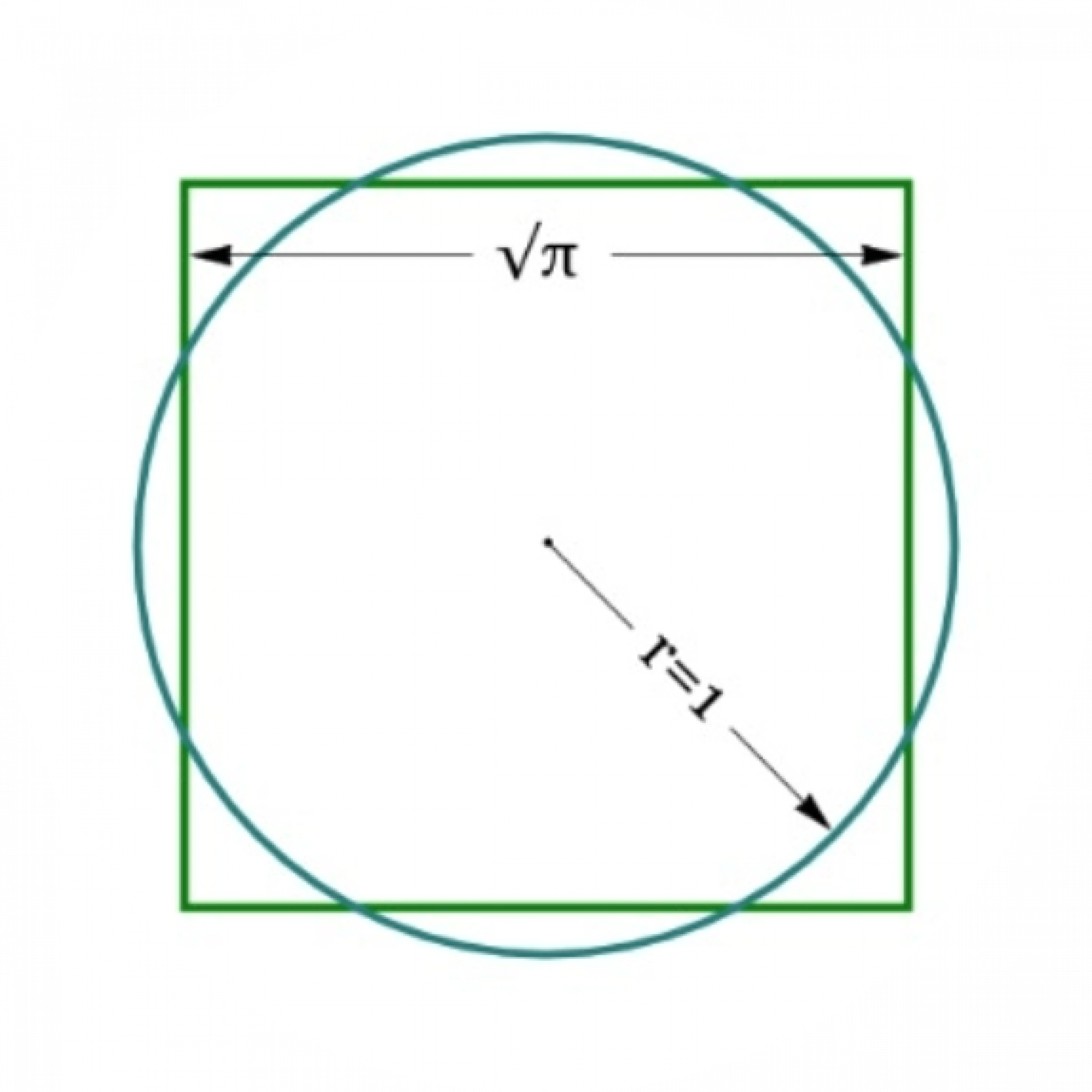
How do you construct a square of the same area as a circle using a compass and a ruler? Impossible, proved the Freiburg mathematics professor Ferdinand von Lindemann in 1882 – thus solving an age-old conundrum of geometry.

Can a walk in the fresh air be of help in solving a centuries-old scientific problem that has frustrated all attempts to do so, even those of ancient thinkers like Anaxagoras (499–428 BC) or the polymath Leonardo da Vinci (1452–1519)? Ferdinand von Lindemann, professor of mathematics at the University of Freiburg between 1877 and 1883,_¹ would have certainly answered in the affirmative. According to his autobiographical notes, he figured out on a walk from Freiburg’s Lorettoberg to Günterstal why squaring the circle – in other words, ‘constructing from a given circle a square with exactly the same area using a compass and an (unmarked) ruler’_² – is an impossible task._³

The reason why squaring the circle does not work has to do with several properties of the mathematical constant pi (π): The ratio of the circumference of a circle to its diameter was calculated approximately by the Greek mathematician Archimedes (ca 287–212 BC), but it is not a rational number. The latter insight goes back to the polymath Johann Heinrich Lambert (1728–1777)._⁴

Lindemann’s achievement was to prove ‘that π is also a transcendental number. This means that there is no polynomial with rational coefficients’_⁵ – such as x³+2x-5 – ‘whose zero is π. It follows that it is in principle impossible to convert a circle into a square of equal area by means of geometric construction steps.’_⁶

Ferdinand von Lindemann is representative of a number of renowned researchers who have contributed to the University of Freiburg’s profile as a centre for significant scientific discoveries from its founding in 1457 to the present day. The mathematician Ferdinand von Lindemann’s achievement is commemorated by an eponymous prize for outstanding dissertations in mathematics, which is still awarded today_.⁷